剑指 Offer 题解 | 26. 树的子结构
力扣

题目描述
判断二叉树 B 与 A 的一个子树是否拥有相同的结构和节点值。(约定空树不是任意一个树的子结构)
复盘
思路
这道题常规思路应该是考虑使用递归(版本 a),不过实际开发过程中,我先用非递归的版本 b 提交通过了……
心得(可能是废话,与此题无关可以略过)
错误率 vs 时间。刷题的时候,不必刻意在意错误率,觉得自己思路对了,该考虑的情况考虑的差不多了,就点击提交按钮吧。时间、精力同样很宝贵,更何况存在诸如 345. 反转字符串中的元音字母这种题,第一次提交的时候果断被坑了没有考虑到大写字母的情况……
更应该注重的,还是题目的解题套路、以及在不断试错过程中的领悟,或者多花一些时间多看看其他大佬们的题解,是不是有新的思路,或者有更好的解法……
在学习的时候,向孩子学习,不害怕犯错~
ps:这道题很有意思的两点是,在做这题的时候,我先跑到隔壁学习了这题 102. 二叉树的层序遍历,然后实现了版本 b;无独有偶,在实现版本 a 的过程中,我又跑到隔壁先实现了 100. 相同的树,再回来做这提,发现思路豁然开朗……
版本 a:递归
前言:如上文所说,在实现版本 a 的过程中,起初我围观了官方的题解,发现代码异常精简… 甚至有点看不明白;然后看到另外一篇题解里提到,可以通过 100. 相同的树这道题衍生过来解决这题,于是我就照做了,果然效果拔群。
强烈建议先做掉 100. 相同的树 这题再来解这道题。
强烈建议先做掉 100. 相同的树 这题再来解这道题。
强烈建议先做掉 100. 相同的树 这题再来解这道题。
那道题很简单。
递归目标
因为整道题的目标是判断两棵树是否相似,
所以递归目标就是判断两个节点是否相似。
递归逻辑
先简单过一下 100. 相同的树的递归逻辑。
那道题是递归判断当前节点、左子树、右子树是否都同时相等。
在实际写判断逻辑的时候,不必考虑如何满足左子树、右子树是否同时相等,那是递归自己去做的事情,
我们只需要考虑当前节点是否相等就好,主要需要考虑一下,A、B 为空子树的情况。
至于左右子树的判断,扔给递归就 ok 了。
1
2
|
// 递归考察左子树、右子树
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);`
|
这道题略有不同,问的是是否相似。于是就会有两个不同点:递归判断条件、递归判断范围
条件不同
相等要求的是对应的节点都相同,不能多也不能少。
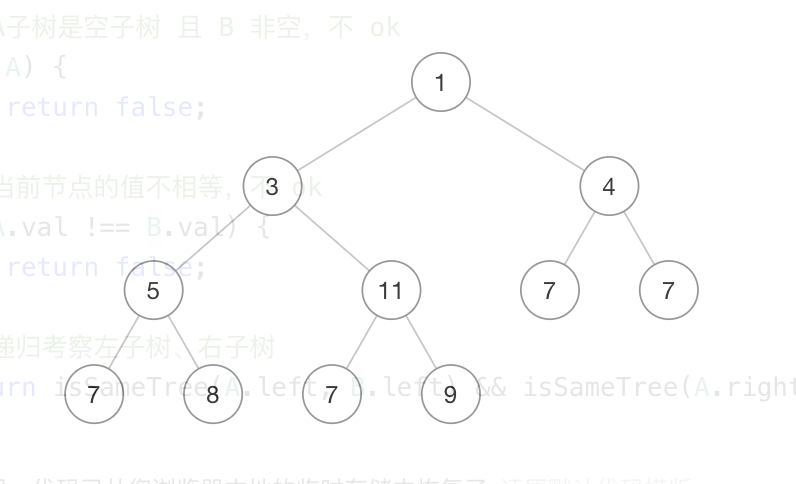
而至于相似,如图

从示例图上可以直观地看出,相似说明 A 可以在 B 结构的基础上有多余的子节点,
即,允许子节点 B === null 的情况,
1
2
3
4
|
// B 子树是空子树就 ok,无论 A 是否为 null
if(!B) {
return true;
}
|
就是这样,
范围不同
相等判断范围的是整棵树完全相同。
而相似判断范围则是 B 与 A 的部分子树相同。
那如何用代码来描述部分子树呢?
或者换一个思路,实际上判断相等时,判断的起点是:A、B 的根节点。
而判断相似,判断的起点变为了:B 的根节点和 A 的任意节点。
所以这里又需要递归来帮忙了…
1
2
3
4
|
var isSubStructure = function(A, B) {
// ...
return isSameTree(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B)
}
|
就是这样,
边界值
题目约定:约定空树不是任意一个树的子结构
所以
1
2
3
4
5
6
7
|
var isSubStructure = function(A, B) {
// 约定空树不是任意一个树的子结构
if(!A || !B) {
return false;
}
return isSameTree(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B)
}
|
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
/**
* @param {TreeNode} A
* @param {TreeNode} B
* @return {boolean}
*/
var isSubStructure = function(A, B) {
// 约定空树不是任意一个树的子结构
if(!A || !B) {
return false;
}
return isSameTree(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B)
};
/**
* @param {TreeNode} A
* @param {TreeNode} B
* @return {boolean}
*/
var isSameTree = function(A, B) {
// B子树是空子树 ok
if(!B) {
return true;
}
// A子树是空子树 且 B 非空,不 ok
if(!A) {
return false;
}
// 当前节点的值不相等,不 ok
if(A.val !== B.val) {
return false;
}
// 递归考察左子树、右子树
return isSameTree(A.left, B.left) && isSameTree(A.right, B.right);
};
|
复杂度分析
时间复杂度
emmmmm 老师我不会……
就考虑最坏情况,如果 B 不是 A 子树
- 第一层递归 isSubStructure,则时间为 O(m) m 为 A 的节点数
- 第二层递归 isSameTree,如果 B 一直不为空就需要一直判断,直到 B 为空为止,所以是 O(n) n 为 B 节点的个数?
所以综合一下就是 O(m * n) ?
空间复杂度
这个真不知道…… (大学学的还给老师了……)
网上的说法是二叉树遍历的空间复杂度取决于树的高度 h,这里最坏情况下就是一条直的树枝没有分叉,所以就是 B 的高度 n,O(n)
版本 b:非递归
这个版本的代码,我个人认为就比较有趣了。
刚开始解这道题时候,我一直在观察测试数据,觉得这道题应该有比较“巧妙”的解法,于是就自己输入了几组测试数据,想找找看有没有什么规律。
1
2
3
4
5
6
|
...
[1,3,4,5,11,7,7,7,8,7,9]
[3,5,11,7,8,null,9]
[4,2,3,4,5,6,7,8,9]
[4,8,9]
...
|
对了这里有小 tip,如下图所示,可以在「测试用例」里点击右侧按钮「树结构可视化」,把输入的树给可视化地展示出来。(ps:计划研究一下他们源码怎么实现的…)

结果好像还真有点规律。
以这组数据为例:
1
2
|
A = [1,3,4,5,11,7,7,7,8,7,9]
B = [3,5,11,7,8,null,9]
|
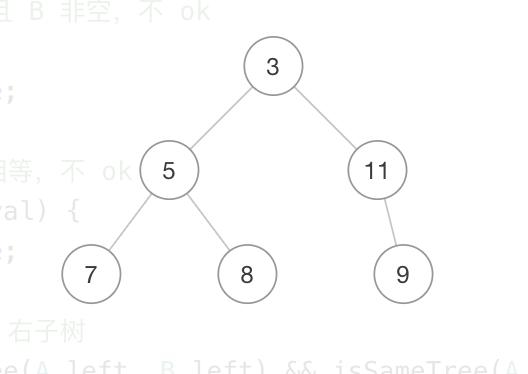
他们的结构图分别是,


可以直观地看出的确,B 是 A 的子结构。
然后我就在研究下标与相差层数的关系:
1
2
3
4
5
6
7
8
|
// #n 表示层数,从 0 开始
#0 B[0] === 3 === A[1] #1
#1 B[1] === 5 === A[3] #2
#1 B[2] === 11 === A[4] #2
#2 B[3] === 7 === A[7] #3
#2 B[4] === 8 === A[8] #3
#2 B[5] === null !=== A[9] #3
#2 B[6] === 9 === A[10] #3
|
得出了一个看似符合规律的结论:
1
|
#q B[j] === A[2^q + j] #p
|
然后问题来了,怎么用代码去验证……?
首先问题是,如何用这种广度优先的方式去遍历呢?
于是去翻了一下 Leetcode 题库,找到了一个叫 102. 二叉树的层序遍历的好东西。
代码直接拿来用的时候发现层序遍历生成的是一个二维数组,但我刚才的推导公式是一个一维扁平化的数组。简单调整了一下,变成了一维。
但发现…… 变成一维以后有个问题,每次还要计算当前项是第几层……这个计算量爆炸吧?
后来转念一想,二维数组里每个数组的索引值不就是记录着层数吗?
于是就用这种方案,改一下我们的算式即可。
1
2
3
4
5
6
7
|
B[0][0] === 3 === A[1][0]
B[1][0] === 5 === A[2][0]
B[1][1] === 11 === A[2][1]
B[2][0] === 7 === A[3][0]
B[2][1] === 8 === A[3][1]
B[2][2] === null !=== A[3][2]
B[2][3] === 9 === A[3][3]
|
所以推导出的算式是:
1
|
B[levelB][indexB] === 9 === A[levelA][indexA]
|
变量显然太多了,而办法也很容易想到:
先遍历 A 找出第一个和 B 相同的节点,作为起点。这样 A[levelA][indexA] 就转化为已知数了。
1
2
3
4
5
6
7
8
9
|
function matchAB(levelOrderA, levelOrderB, levelA, i) {
// 确定 root 位置 levelOrderA[levelA][i]
if(levelOrderA[levelA][i] !== levelOrderB[0][0]) {
return false;
}
// ...
// ...
}
|
所以推导出的算式也要变一下:
1
2
3
4
|
// 找到第 l 层第 i 个元素为待匹配的 A 子树的起点
levelOrderA[l][i] === levelOrderB[0][0]
// 去判断 A[l + levelB][i + indexB] 是否与 B[levelB][indexB] 相同
B[levelB][indexB] === ? === A[l + levelB][i + indexB]
|
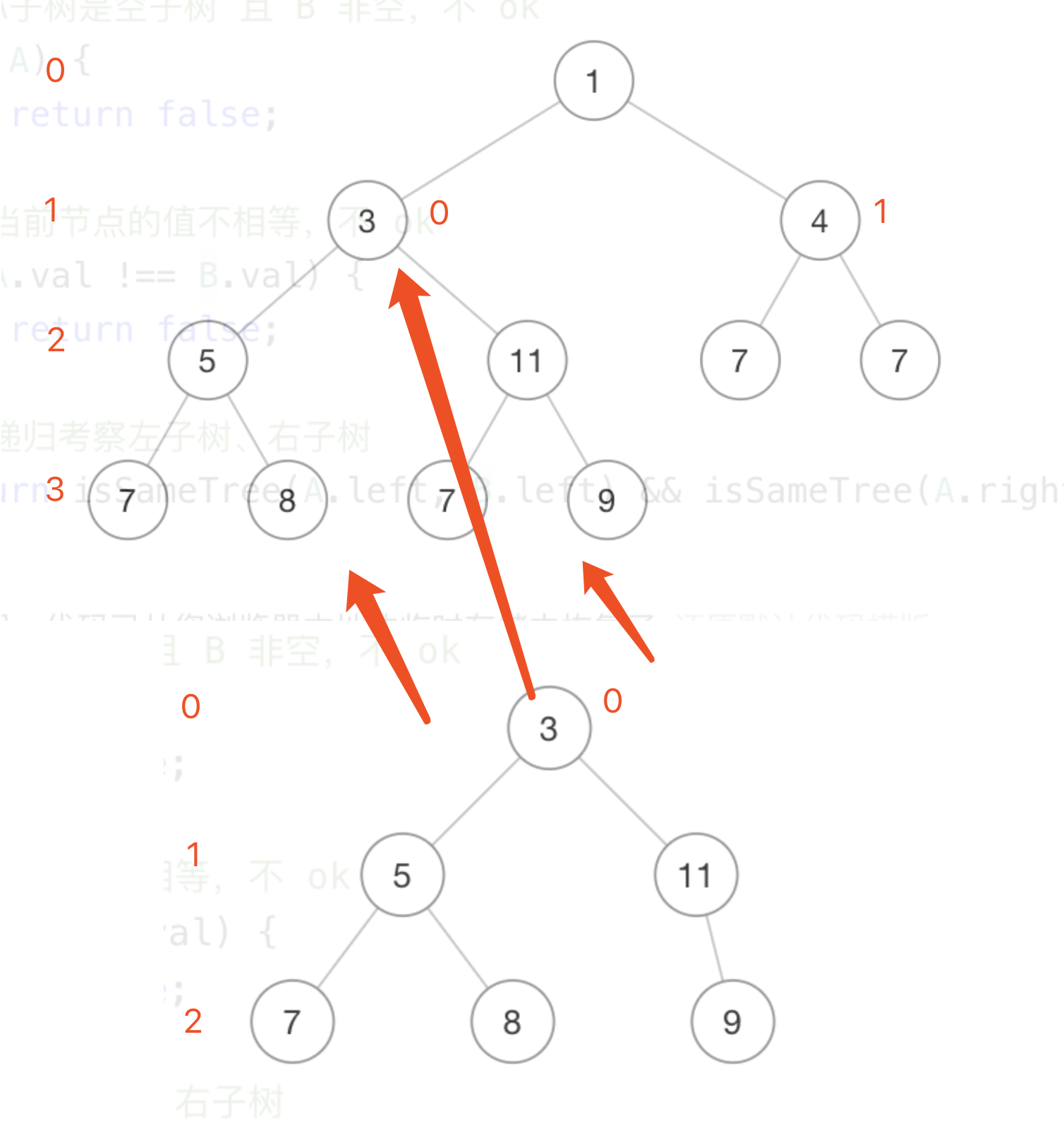
这个等式对照着图就很好理解:(或者其实看图想出这个思路可能更快一点)

核心逻辑就是这个,余下的就是边界值的判断了,主要就是分别考察一下 A、B 为空节点的情况。
但是由于是二维数组,所以务必也要注意一下 A[levelA][indexA] 中 levelA 为空的情况,即 B 节点在 A 中的映射位置超过了 A 的最大高度的情况…(别问我怎么知道的……说多了都是 WA)
所以剩下的逻辑不再赘述了,版本 b 的代码里也有注释,以及关键位置的 console.log 信息,感兴趣的同学可以跑跑玩玩~
复杂度分析
性能方面,起初对这套版本 b 的代码我是不抱希望的,甚至担心会超时或者内存爆表…
因为我先对 A 和 B 分别进行了一次层序遍历,其次最坏情况下,会遍历 A * B……所以……
结果却还出乎意料的不算特别慢……

时间复杂度
层序遍历:O(m) + O(n),m、m 分别是 A、B 的节点个数
判断相似:O(m * n)
所以总体上是:O(m * n) + O(m) + O(n)
空间复杂度
层序遍历:O(m) + O(n),m、m 分别是 A、B 的节点个数
判断相似:O(m) + O(n) ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
/**
* @param {TreeNode} A
* @param {TreeNode} B
* @return {boolean}
*/
var isSubStructure = function(A, B) {
if(!A || !B) {
return false;
}
const levelOrderA = levelOrder(A);
// console.log(levelOrderA)
const levelOrderB = levelOrder(B);
// console.log(levelOrderB)
return checkSubStructure(levelOrderA, levelOrderB)
};
// checkSubStructure
function checkSubStructure(levelOrderA, levelOrderB) {
// console.log(levelOrderA, levelOrderB)
for(let levelA = 0; levelA < levelOrderA.length; levelA ++) {
for (let i = 0; i < levelOrderA[levelA].length; i++) {
if(matchAB(levelOrderA, levelOrderB, levelA, i)) {
return true;
}
}
}
return false;
}
//
function matchAB(levelOrderA, levelOrderB, levelA, i) {
// 确定 root 位置 levelOrderA[levelA][i]
if(levelOrderA[levelA][i] !== levelOrderB[0][0]) {
return false;
}
// 从第"1"层开始计算
for(let levelB = 1; levelB < levelOrderB.length; levelB++) {
for (let j = 0; j < levelOrderB[levelB].length; j++) {
// console.log('levelA', levelA, i, levelOrderA[levelA + levelB])
// console.log('levelB', levelB, j, levelOrderB[levelB])
if(!levelOrderA[levelA + levelB]) {
return false;
}
// console..log(levelOrderB[levelB][j], levelOrderA[levelA + levelB][i + j])
if(levelOrderB[levelB] !== null
&& levelOrderA[levelA + levelB] !== null
&& levelOrderB[levelB][j] !== null
&& levelOrderB[levelB][j] !== levelOrderA[levelA + levelB][i + j]) {
return false;
}
}
}
return true;
}
// bfs
function levelOrder(root) {
const ret = [];
if (!root) return ret;
const q = [];
q.push(root);
while (q.length !== 0) {
const currentLevelSize = q.length;
ret.push([]);
for (let i = 1; i <= currentLevelSize; ++i) {
const node = q.shift();
if(node) {
ret[ret.length - 1].push(node.val);
} else {
ret[ret.length - 1].push(null);
continue;
}
// 只要有子树,就继续
if (node.left || node.right) {
q.push(node.left);
q.push(node.right);
}
}
}
return ret;
};
|
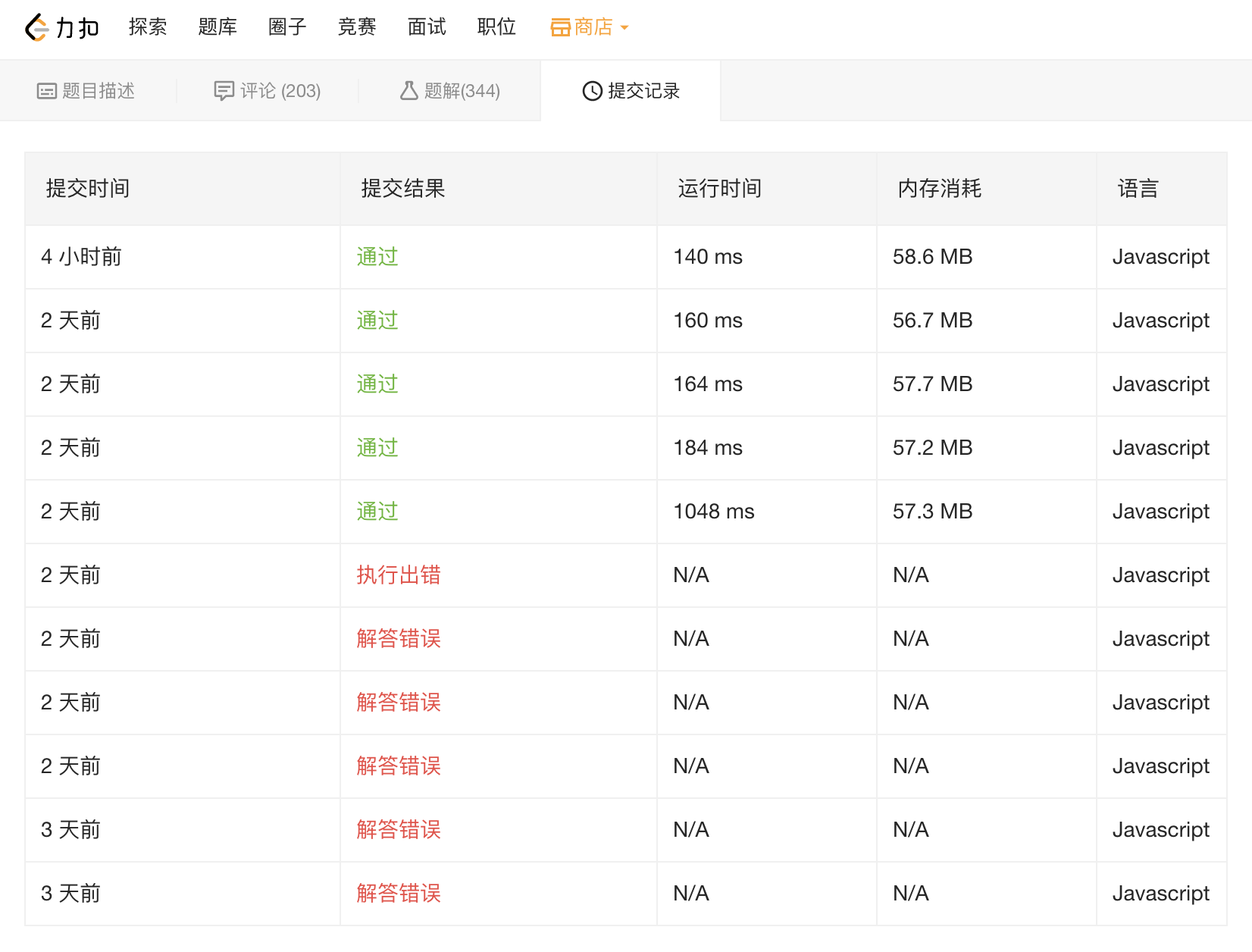
统计
| 版本 |
耗时 |
超越 |
内存 |
超越 |
更新时间 |
| a 1.0.0 |
140ms |
15.84% |
58.6MB |
100% |
2020年07月15日20:00:00 |
| b 1.0.0 |
180ms |
7.04% |
57.2MB |
100% |
2020年07月14日22:00:00 |
数据来自 leetcode-cn.com 提交记录

后记
写完这篇题解后,又想到开篇里提到的不要害怕提交解答错误的问题,除了前文提到的,
在学习的时候,向孩子学习,不害怕犯错~
还想再补充一句,
在工作的时候,再怎么缜密也不为过~
所以结论是在不同场景(学习、工作)下,要切换不同的战斗模式 =。=
好了,回到这次题解的代码层面,至于哪个版本代码更喜欢,个人选 a,代码是真的简洁,可读性好(配上注释)…… 递归真的香…
然后对于版本 b,如果先在纸上画出 A 和 B 的映射关系,标注好层级应该能够更快地找出思路。
还有件有趣的发现,回过头来看这道题目的版本 a,返回值其实就是前序遍历。
return isSameTree(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B)
如果有难以理解、有错误的地方欢迎各位大佬指出
感谢读到这里~
以上
参考资料
题解




 清风迅来
清风迅来