105. Construct Binary Tree from Preorder and Inorder Traversal (Medium)

Tony.Xu 收录于题解每周一题

2020-07-08 约 3333 字预计阅读 7 分钟次阅读

LeetCode | 力扣

LeetCode 题解 | 从前序与中序遍历序列构造二叉树

前言：毕业后头一回这么认真写题解，话可能有点多，如果有难以理解、有误的地方欢迎各位大佬指出

题目描述

根据一棵树的前序遍历与中序遍历构造二叉树（假定无重复值）

复盘

这题主要考察了两点：

数据结构：二叉树、前序遍历、中序遍历的定义
算法：递归（分治思想）

数据结构

1
2
3
4
5
6
7
8


/**
 * 二叉树：根节点，左子树，右子树
 */
export interface ITreeNode {
  root: number; // 根
  left: ITreeNode | null; // 左子树
  right: ITreeNode | null; // 右子树
}

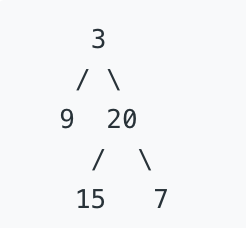
前序遍历：根、左、右 —— [3,9,20,15,7]

中序遍历：左、根、右 —— [9,3,15,20,7]

算法

递归

定义：把原问题拆解成若干个与原问题结构相同但规模更小的子问题，待子问题解决以后，原问题就得以解决。

说人话：好比拼 100*100 的拼图，拆成拼 100 份 10*10 的拼图，等 100 份子拼图拼完后，原拼图也拼完了（假设每个子拼图素材完备）。

在复盘这道题时，我是这么拆解这题的递归过程的：递归目标、递归逻辑、递归参数、初始状态、结束状态

注：下面的版本 a 和版本 b 都是我看了答案后做的复盘，而在看别人的题解和代码的时候，可以同时用测试数据代入进去（重点可以运行一下第一、第二步以及最后两步），会有更直观的感受。

版本 a

在参考了力扣的官方视频题解后，完成了版本 a

递归目标

整道题的最终目标是构建一棵树，用递归的思想，要把一棵树拆成结构相同但规模更小，那就是构建树的一个节点。

所以，子问题就是：返回下一个节点 ITreeNode（根，左子树，右子树），直到叶子节点结束

递归逻辑

我们知道了递归的目标是找到当前节点的下一个节点，而由节点的定义可知，构建一个节点需要确定三个成员：根、左子树、右子树。

所以每一次递归的逻辑实际上就是寻找：

找前序的根。找到根节点 —— 前序遍历的第一个元素
找中序的根。根据前序遍历根节点的值，找到中序遍历中对应的元素 —— 题目告知节点的值不会重复，所以能根据前序遍历的根节点一一对应到中序遍历的根节点
找前序、中序的左、右子树。根据中序遍历的根节点（左子树、根、右子树），确定前序遍历、中序遍历各自的左子树、右子树（各自起始位置、结束位置）
重复以上步骤直到叶子节点结束

递归参数

根据递归逻辑，可以得知，只要确定了前序遍历、中序遍历的根节点，前序、中序的左、右子树（各自起始位置、结束位置），就可以确定下一个节点。

所以递归参数：preorder、preLeft、preRight、inorder、inLeft、inRight、map

引入 map 来记录 inorder 值与下标的映射，从而优化根据前序遍历根节点的值，找到中序遍历中对应的元素的速度

初始状态

方法

在纸上画出第一次的初始状态

1
2
3
4
5
6
7



preLeft = 0
preRight = preorder.length - 1
inLeft = 0
inRight = inorder.length - 1
buildSubtree(preorder, preLeft, preRight, inorder, inLeft, inRight, map)

结束条件

方法

先在纸上画出最后一次递归的情况
再在纸上画出倒数第二次的情况

通过第1、2步，可以得出递归终止的条件

说明

最后一次递归即叶子节点，子树为空，即 preorder 在 [preLeft, preRight] 区间内长度为 0，而如果 preLeft === preRight 表示当前节点并不是叶子节点，仍有 1 个子节点（叶子节点）。
由第一步可知，倒数第二次时，preLeft === preRight

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    var preLen = preorder.length;
    var inLen = inorder.length;

    if(preLen !== inLen) {
        return null;
    }

    // hash map 中序遍历
    var map = {};
    for (var i = 0; i < inLen; i++) {
        map[inorder[i]] = i;
    }
    // 初始状态
    // 前序：根 0，左 1~x，右 x+1~len
    // 中序：左，0~inRootIndex-1,中 inRootIndex map[pre[0]]，右 c+1~len
    return buildSubtree(preorder, 0, preLen - 1, inorder, 0, inLen - 1, map)
};

/**
 * 构建下一个节点
 * @param: preorder 前序遍历
 * @param: preLeft 前序遍历左边界
 * @param: preRight 前序遍历右边界
 * @param: inorder 中序遍历
 * @param: inLeft 中序遍历左边界
 * @param: inRight 中序遍历右边界
 * @param: map 中序遍历映射
 */
function buildSubtree(preorder, preLeft, preRight, inorder, inLeft, inRight, map) {
    if(preLeft > preRight || inLeft > inRight) {
        return null;
    }
    var treeNode = {}
    // 前序遍历的根节点对应 —— 该值 map 到的中序遍历的下标
    var inRootIndex = map[preorder[preLeft]];
    // 前序遍历，左子树的最后一位索引值 x
    // x - (preLeft + 1) === (inRootIndex - 1) - inLeft => x = inRootIndex + preLeft - inLeft
    var x = inRootIndex + preLeft - inLeft;
    treeNode.val = preorder[preLeft];
    treeNode.left = buildSubtree(preorder, preLeft + 1, x, inorder, inLeft, inRootIndex - 1, map );
    treeNode.right = buildSubtree(preorder, x + 1, preRight, inorder,  inRootIndex + 1, inRight, map);
    // console.log(treeNode)
    return treeNode;
}

复杂度分析

时间复杂度

O(n) 其中 n 是树中的节点个数。

空间复杂度

O(n) 返回的答案 O(n) + 哈希 map O(n) + 每次遍历时 var x = inRootIndex + preLeft - inLeft; O(n)？，其中 n 是树中的节点个数

版本 b

早上我在查看代码运行速度排名图表时，无意间看到鼠标样式变成手型了，于是点了一下

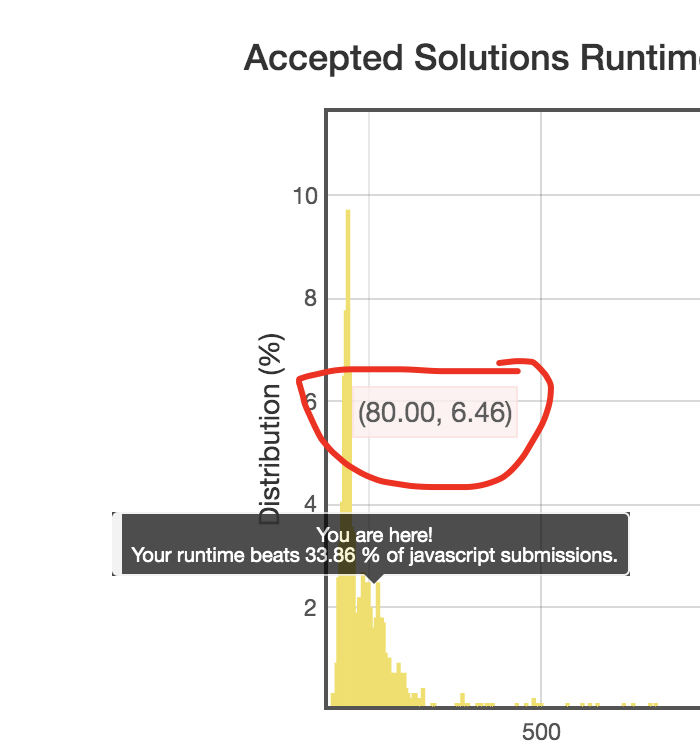
结果弹出来了一份代码……

看到这份代码比我快，而且又很简洁，于是就想研究研究.

递归逻辑

友情提示：如果感觉下面的文字有点绕，可以先略过看看下一部分的内容

取`前序根节点`，并移除该`根节点`

在说递归逻辑之前，先想象一下，不断地移除前序遍历的第一个元素，会发生什么？

根据[根、左、右]的定义，可知会先移除根节点，然后是左子树，最后是右子树。

举个例子，上图前序遍历：根、左、右 —— [3,9,20,15,7]

第一次移除根 3、第二次左 9、第三次就是右 20 了，然后再移除左 15，最后移除右 7

所以每一次递归，前序遍历移除第一个元素后，可以保证余下序列第一个元素始终是前序遍历根节点，且只有2种可能：

左子树的根节点
右子树的根节点

从而就不需要额外的参数去记录前序遍历的根节点的下标了，直接 preorder.shift() 即可。

找`中序对应的根节点`

而对于这道题，题目条件给出了中序遍历，根据定义，前序遍历的根节点是与中序遍历的根节点一一对应，从而可以得出中序遍历根节点的左、右子树明确的范围。

构建`左子树`、`右子树`

又因为定义：前序 [根、左、右]，中序 [左、根、右]

前序的左、右子树的长度和中序左、右子树的长度也是一致的，所以当中序遍历的左、右子树构建完成后，对应的前序遍历左、右子树也一样完成了。

所以这个时候，与版本 a 不同，我们转换思路，不去考虑前序遍历的左、右子树边界，只考虑中序遍历的左右子树边界，而当中序遍历的左、右子树为 null 时，这个节点就构建完成了。

小结

所以步骤就是：

取前序根节点，并移除该根节点
找中序对应的根节点
构建左子树
重复以上步骤直到没有左子树
构建右子树
重复以上步骤直到没有右子树
结束

ps：这道题用这个递归逻辑也可以很方便地解决 106.construct-binary-tree-from-inorder-and-postorder-traversal 这题。

递归参数

preorder（会变）、inorder、start、end、map

引入 map 来优化
start 记录中序遍历的左子树开始位置
end 记录中序遍历的右子树结束位置

初始状态

方法

在纸上画出第一次的初始状态

1
2
3
4
5



start = 0
end = inorder.length - 1
buildSubtree(preorder, inorder, start, end, map)

结束条件

方法

先在纸上画出最后一次递归的情况
再在纸上画出倒数第二次的情况

通过第1、2步，可以得出递归终止的条件

说明

最后一次递归即叶子节点，子树为空，即 inorder 在 [start, end] 区间内长度为 0，而如果 start === end 表示当前节点并不是叶子节点，仍有 1 个子节点（叶子节点）。
由第一步可知，倒数第二次时，start === end

AC 代码

2020年07月10日09:00:00

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54


/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
  if (preorder.length !== inorder.length) {
    return null;
  }
  const map = {};
  for(let i = 0; i < inorder.length; i++) {
    map[inorder[i]] = i;
  }
  return buildSubtree(preorder, inorder, 0, preorder.length -1, map)
};

/**
 * @param: preorder
 * @param: inorder
 * @param: start `中序遍历`的左子树开始位置
 * @param: end `中序遍历`的右子树结束位置
 * @param: map
 */
var buildSubtree = function(preorder, inorder, start, end, map) {
    // start === end 时为叶子节点,
    // start > end 表示 null
    if ( start > end) {
      return null;
    }

    let val = preorder.shift();
    // 前序遍历
    let root = new TreeNode(val);

    // 中序遍历对应的根节点
    let index = map[val];

    // 递归全部左子树
    root.left = buildSubtree(preorder, inorder, start, index -1, map);
    // 递归全部左子树
    root.right = buildSubtree(preorder, inorder, index +1, end, map);

    return root;

};

复杂度分析

时间复杂度

O(n) 其中 n 是树中的节点个数。

ps：preorder.shift(); 这个的复杂度未知…… 但版本 b 的速度比版本 a 的快 60ms，所以应该也是 O(n) 吧…… 可能内部有优化？

空间复杂度

O(n) 返回的答案 O(n) + 哈希 map O(n) + 每次遍历时 let index = map[val]; O(n)？，其中 n 是树中的节点个数

统计

版本	耗时	超越	内存	超越	更新时间
a 1.0.0	136ms	33.86%	39.3MB	39.18%	2020年07月08日20:00:00
b 1.0.0	72ms	96.35%	40.5MB	34.13%	2020年07月10日09:00:00

数据来自 leetcode.com 提交记录

参考资料

力扣官方视频题解

Leetcode 提交记录

总结

写完这篇题解后，感觉解这道题的关键主要还是在于~~看答案~~理解 + 利用定义

前序遍历（根、左、右）
中序遍历（左、根、右）

至于递归逻辑，在纸上画画图，手动算两轮测试数据，有很大的帮助。

如果有难以理解、有错误的地方欢迎各位大佬指出

感谢读到这里~

以上

目录

105. Construct Binary Tree from Preorder and Inorder Traversal (Medium)

LeetCode 题解 | 从前序与中序遍历序列构造二叉树

题目描述

复盘

数据结构

算法

递归

版本 a

递归目标

递归逻辑

递归参数

初始状态

方法

结束条件

方法

说明

代码

复杂度分析

时间复杂度

空间复杂度

版本 b

递归逻辑

取前序根节点，并移除该根节点

找中序对应的根节点

构建左子树、右子树

小结

递归参数

初始状态

方法

结束条件

方法

说明

AC 代码

复杂度分析

时间复杂度

空间复杂度

统计

参考资料

总结

取`前序根节点`，并移除该`根节点`

找`中序对应的根节点`

构建`左子树`、`右子树`