46. 全排列（中等）

Tony.Xu 收录于题解

2020-08-14 约 1535 字预计阅读 4 分钟次阅读

力扣

这道题是我在解 N 皇后问题，在抄答案时看到答案先用这道题来讲述回溯法的原理。

强烈推荐大家去围观一下 labuladong 大佬的这篇题解，可能是全网讲解回溯法最清晰的了，而且给出的回溯法解题模板真的很实用。

结论

先直接给出结论

注：以下内容大部分都是摘抄、整理自 labuladong 大佬的这篇题解。

回溯法解题套路 —— backtrack 框架

每次解回溯题时，把以下内容复制一下，照着这个模板去写就行

1
2
3
4
5
6
7
8
9


- 触发结束条件
- for 选择 in 选择列表:
  - # 做选择
    - 将该选择从选择列表移除
    - 路径.add(选择)
  - backtrack(路径, 选择列表)
  - # 撤销选择
    - 路径.remove(选择)
    - 将该选择再加入选择列表

而这个模板中，主要考虑三件事情：

结束条件：到达决策树底层，无再做选择的条件
选择路径：已经做出的选择
选择列表：当前可以做的选择

本题应用

1
2
3
4
5
6
7
8


- 路径长度等于选择列表长度，记录本次路径
- for 选择 in 选择列表
  - # 做选择
    - 判断当前值是否存在于路径中，如果是，跳过本次循环
    - 路径.push(选择)
  - backtrack(路径，选择列表)
  - # 撤销选择
    - 路径.pop(选择)

回溯法

回过头来，简单说一说回溯法的定义，如果觉得难以理解可以继续往下看。

回溯法的本质是遍历一棵决策树。可以简单理解为优化版的暴力遍历。

普通的暴力遍历，每一次遍历都是从树的根节点出发，遍历到叶子节点时，重新回到树的根节点开始第二次遍历。

回溯法，遍历到叶子节点时，会返回到它的父节点，看是否还有其他决策，如果存在，则在新的决策子树上继续遍历。

题目描述

如果动笔手动画一下 [1,2,3,4] 的全排列，通常为了避免遗漏，我们会采用定一动一的方式：

先固定首位 1，接下来有三种选择： 2、3、4
- 再接着固定第二位 2，接下来剩下两种选择：3、4
  - …
- 返回第二级，再接着固定第二位 3，接下来剩下两种选择：2、4
  - …
- …
返回第一级，固定首位 2，接下来有三种选择：1、3、4
- …
…

其实这里就已经使用了回溯法的思想。

而如果是普通暴力法，则会是

先固定首位 1，接下来有三种选择： 2、3、4
- 再接着固定第二位 2，接下来剩下两种选择：3、4
  - 固定第三位 3，接下来只有 1 种选择
    - 固定第四位 4，结束
固定首位 1，接下来有三种选择：2、3、4
- 再接着固定第二位 2，接下来剩下两种选择：3、4
  - 固定第三位 4，接下来只有 1 种选择
    - 固定第四位 3，结束
…

可见回溯的过程节省下了许多重复的计算量（但仍然属于暴力法遍历的范畴内）

题解说明

这次题解大部分注释都是原答案提供的，部分注释是我将 C 代码用 JavaScript 实现过程中的一些标注。

友情提醒：要注意 JavaScript 中的引用值类型问题。

另外，原题解是使用了全局变量来记录 res，当我也想这么尝试的时候，题目告诉我 Wrong Answer，看起来似乎是 LeetCode 的 bug？上一次跑测试用例用的全局变量在新的测试用例里不会重置。

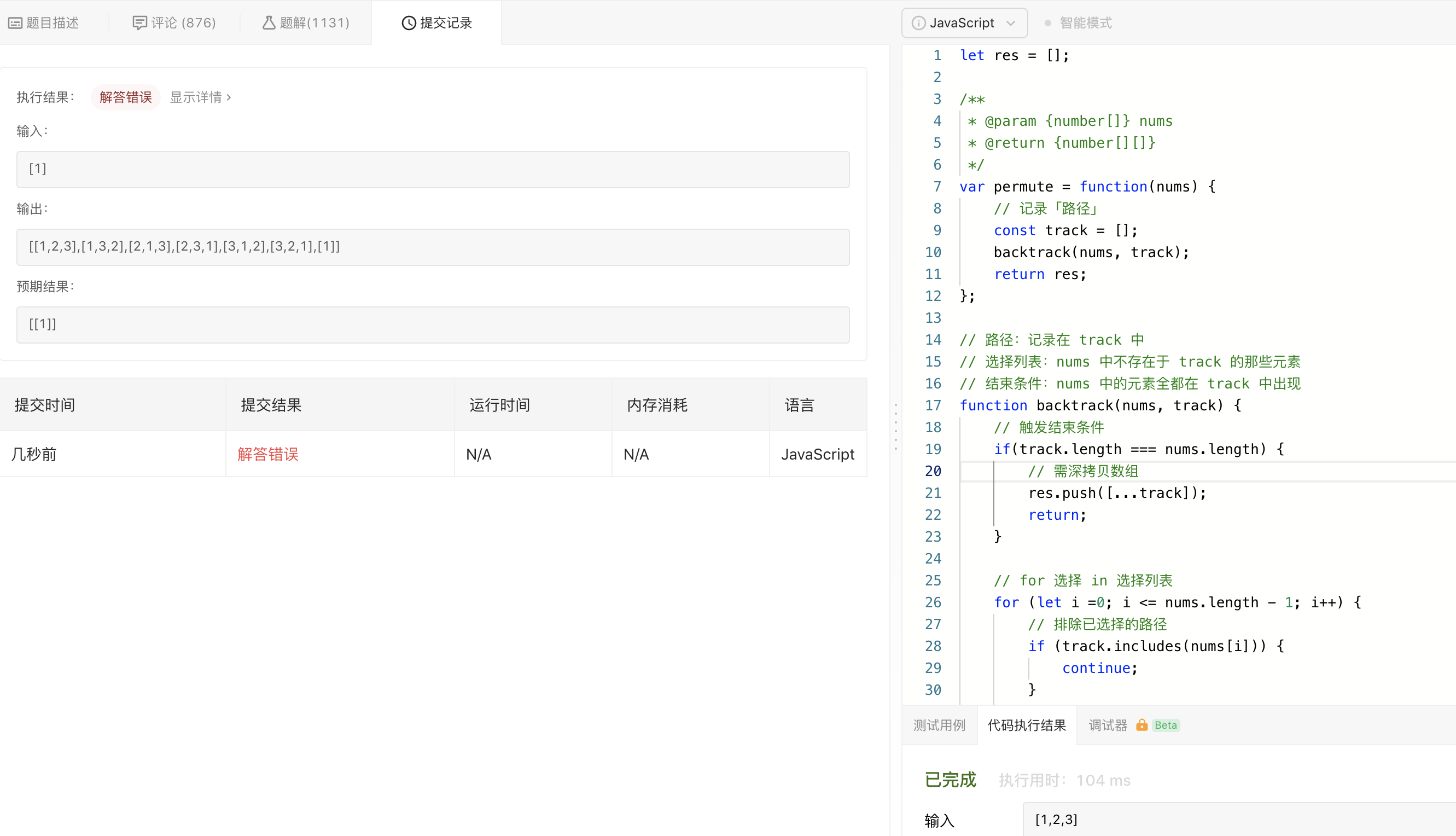
仔细看左侧执行结果，输入 [1]，居然返回了 [1,2,3] + [1] 全排列结果之和……

v 1.0.0

2020年08月14日

统计

版本	耗时	超越	内存	超越	更新时间
1.0.0	144 ms	0%	40.5 MB	87.15%	2020年08月14日18:30:00

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53


/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
    const res = [];
    // 记录「路径」
    const track = [];
    backtrack(nums, track, res);
    return res;
};

// 路径：记录在 track 中
// 选择列表：nums 中不存在于 track 的那些元素
// 结束条件：nums 中的元素全都在 track 中出现
function backtrack(nums, track, res) {
    // 触发结束条件
    if(track.length === nums.length) {
        // 需深拷贝数组
        res.push([...track]);
        return;
    }

    // for 选择 in 选择列表
    for (let i =0; i <= nums.length - 1; i++) {
        // 排除不合法选择 —— 已选择的路径
        if (track.includes(nums[i])) {
            continue;
        }

        // 做选择
        track.push(nums[i]);
        backtrack(nums, track, res);

        // 撤销选择
        track.pop();

    }
}

/**
 * backtrack 框架
 *
 * 触发结束条件
 * for 选择 in 选择列表:
 *   # 做选择
 *   将该选择从选择列表移除
 *   路径.add(选择)
 *   backtrack(路径, 选择列表)
 *   # 撤销选择
 *   路径.remove(选择)
 *   将该选择再加入选择列表
 */

目录